How to Determine Rate Law in Chemical Kinetics

How to determine rate law is a fundamental concept in chemical kinetics, a branch of chemistry that explores the rates and mechanisms of chemical reactions. Understanding rate laws allows us to predict how fast a reaction will proceed under different conditions, which is crucial for optimizing chemical processes, designing new catalysts, and unraveling the intricate steps involved in chemical transformations.

Rate laws are mathematical expressions that describe the relationship between the rate of a reaction and the concentrations of the reactants. They provide a quantitative framework for understanding the factors that influence reaction rates, such as temperature, concentration, and the presence of catalysts. By determining the rate law for a particular reaction, we can gain valuable insights into its mechanism, the steps involved in the reaction, and the relative importance of different reactants.

Introduction to Rate Laws

Rate laws are mathematical expressions that describe the relationship between the rate of a chemical reaction and the concentrations of the reactants. They are essential tools in chemical kinetics, providing insights into the mechanism and speed of chemical reactions.

Rate laws are crucial for understanding reaction mechanisms because they reveal the elementary steps involved in a reaction. By examining the rate law, chemists can determine the order of each reactant, which indicates how many molecules of each reactant participate in the rate-determining step of the reaction.

Examples of Rate Laws

Rate laws can be expressed in various forms, depending on the order of the reaction. Here are some common examples:

For a reaction A → Products, the rate law is:
Rate = k[A]ⁿ
where:
k is the rate constant,
[A] is the concentration of reactant A,
n is the order of the reaction with respect to A.

Zero-Order Reactions

Zero-order reactions have a rate that is independent of the concentration of the reactants. This means that the rate of the reaction remains constant, regardless of the amount of reactants present.

Rate = k

First-Order Reactions

First-order reactions have a rate that is directly proportional to the concentration of one reactant. Doubling the concentration of the reactant doubles the rate of the reaction.

Rate = k[A]

Second-Order Reactions

Second-order reactions have a rate that is proportional to the square of the concentration of one reactant or the product of the concentrations of two reactants.

Rate = k[A]² or Rate = k[A][B]

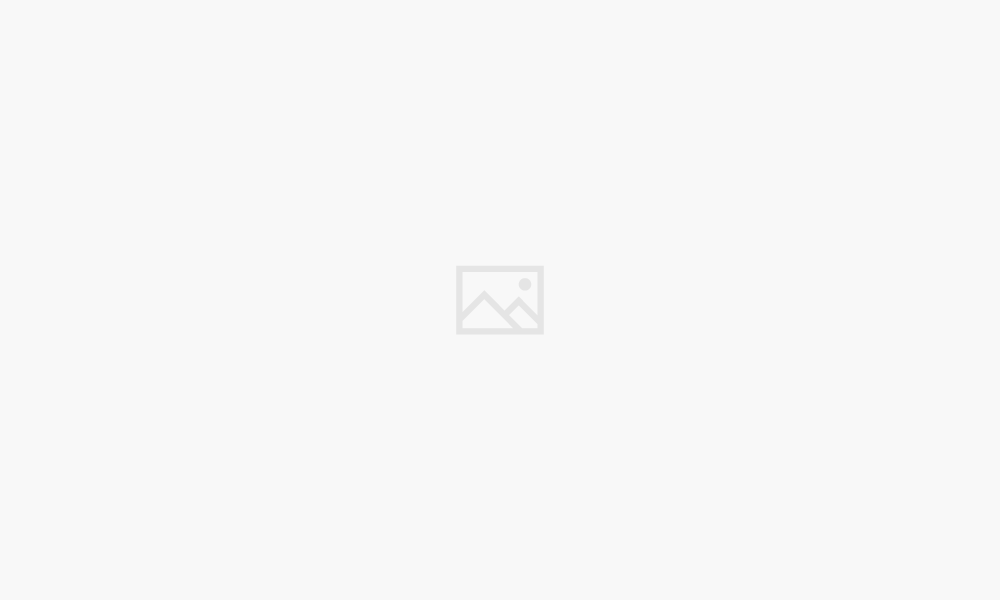
Determining the Rate Law Experimentally

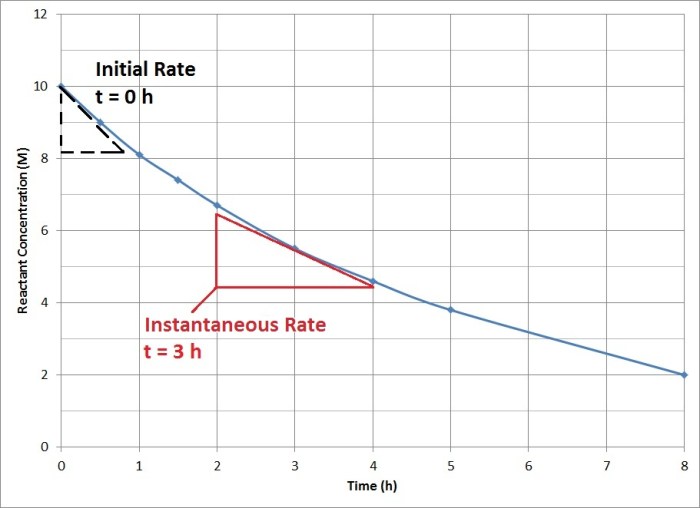
The rate law for a reaction describes how the rate of the reaction changes with the concentrations of the reactants. It is an essential part of understanding the kinetics of a chemical reaction, as it allows us to predict how the rate of a reaction will change under different conditions. There are several methods for determining the rate law experimentally, but one of the most common is the method of initial rates.

The Method of Initial Rates

The method of initial rates is a technique used to determine the order of a reaction with respect to each reactant. It involves measuring the initial rate of the reaction at different starting concentrations of the reactants. By comparing the initial rates at different concentrations, we can deduce the order of the reaction with respect to each reactant.

• The initial rate of a reaction is the rate of the reaction at the very beginning of the reaction, when the concentrations of the reactants are at their highest.
• The order of a reaction with respect to a particular reactant is the exponent to which the concentration of that reactant is raised in the rate law.

Here is a step-by-step guide on how to apply the method of initial rates:

1. Perform a series of experiments: Carry out a series of experiments, each with a different initial concentration of one reactant while keeping the concentrations of the other reactants constant.
2. Measure the initial rate of the reaction: For each experiment, measure the initial rate of the reaction. This can be done by monitoring the change in concentration of a reactant or product over a short period of time at the beginning of the reaction.
3. Compare the initial rates: Compare the initial rates from the different experiments. Look for patterns in how the initial rate changes as the concentration of the reactant of interest changes. For example, if doubling the concentration of a reactant doubles the initial rate, then the reaction is first order with respect to that reactant. If doubling the concentration of a reactant quadruples the initial rate, then the reaction is second order with respect to that reactant. If doubling the concentration of a reactant has no effect on the initial rate, then the reaction is zero order with respect to that reactant.
4. Determine the rate law: Once you have determined the order of the reaction with respect to each reactant, you can write the rate law for the reaction. The rate law will be of the form:
   

   Rate = k[A]^m[B]ⁿ

   where:

   • k is the rate constant
   • A and B are the reactants
   • m and n are the orders of the reaction with respect to A and B, respectively.

Limitations of the Method of Initial Rates

The method of initial rates is a powerful tool for determining the rate law of a reaction, but it does have some limitations:

• It can be difficult to measure the initial rate accurately, especially if the reaction is very fast or very slow. If the reaction is too fast, it may be difficult to measure the concentration of the reactants before they have reacted significantly. If the reaction is too slow, it may take a long time to measure a significant change in concentration.
• The method of initial rates assumes that the reaction is elementary. This means that the rate law can be directly determined from the stoichiometry of the reaction. However, many reactions are not elementary and involve multiple steps. In these cases, the method of initial rates may not be able to accurately determine the rate law. For example, if a reaction involves a fast step followed by a slow step, the rate law will be determined by the slow step, even though the stoichiometry of the fast step may be different.
• The method of initial rates can be time-consuming, especially if you need to perform multiple experiments to determine the order of the reaction with respect to each reactant.

Integrated Rate Laws

The rate law describes how the rate of a reaction depends on the concentrations of the reactants. However, it does not directly tell us how the concentration of a reactant changes over time. To understand this, we need integrated rate laws. Integrated rate laws are mathematical expressions that relate the concentration of a reactant to time. They are derived from the differential rate laws and provide a more direct way to analyze the kinetics of a reaction.

Derivation of Integrated Rate Laws, How to determine rate law

The integrated rate laws for different orders of reactions are derived by integrating the differential rate laws.

Zero-Order Reactions

For a zero-order reaction, the rate of the reaction is independent of the concentration of the reactant. The differential rate law is:

Rate = k

where k is the rate constant.

To derive the integrated rate law, we integrate both sides of the differential rate law with respect to time:

∫d[A] = ∫k dt

where [A] is the concentration of the reactant at time t.

Integrating both sides, we get:

[A] – [A]₀ = -kt

where [A]₀ is the initial concentration of the reactant.

Rearranging the equation, we obtain the integrated rate law for a zero-order reaction:

[A] = -kt + [A]₀

This equation is in the form of a straight line (y = mx + c), where:

* y = [A]
* m = -k
* x = t
* c = [A]₀

Therefore, a plot of [A] versus t for a zero-order reaction will give a straight line with a slope of -k and a y-intercept of [A]₀.

First-Order Reactions

For a first-order reaction, the rate of the reaction is directly proportional to the concentration of the reactant. The differential rate law is:

Rate = k[A]

To derive the integrated rate law, we integrate both sides of the differential rate law with respect to time:

∫d[A]/[A] = ∫k dt

Integrating both sides, we get:

ln[A] – ln[A]₀ = -kt

where ln represents the natural logarithm.

Rearranging the equation, we obtain the integrated rate law for a first-order reaction:

ln[A] = -kt + ln[A]₀

This equation is also in the form of a straight line (y = mx + c), where:

* y = ln[A]
* m = -k
* x = t
* c = ln[A]₀

Therefore, a plot of ln[A] versus t for a first-order reaction will give a straight line with a slope of -k and a y-intercept of ln[A]₀.

Second-Order Reactions

For a second-order reaction, the rate of the reaction is proportional to the square of the concentration of the reactant. The differential rate law is:

Rate = k[A]²

To derive the integrated rate law, we integrate both sides of the differential rate law with respect to time:

∫d[A]/[A]² = ∫k dt

Integrating both sides, we get:

1/[A] – 1/[A]₀ = kt

Rearranging the equation, we obtain the integrated rate law for a second-order reaction:

1/[A] = kt + 1/[A]₀

This equation is also in the form of a straight line (y = mx + c), where:

* y = 1/[A]
* m = k
* x = t
* c = 1/[A]₀

Therefore, a plot of 1/[A] versus t for a second-order reaction will give a straight line with a slope of k and a y-intercept of 1/[A]₀.

Using Integrated Rate Laws to Determine Rate Constant and Half-Life

The integrated rate laws can be used to determine the rate constant (k) and the half-life (t_1/2) of a reaction.

Determining the Rate Constant

The rate constant can be determined from the slope of the linear plot obtained by plotting the appropriate function of concentration versus time. For example, for a first-order reaction, the rate constant is equal to the negative of the slope of the plot of ln[A] versus t.

Determining the Half-Life

The half-life of a reaction is the time it takes for the concentration of a reactant to decrease to half its initial value. The half-life can be calculated from the integrated rate laws.

For a zero-order reaction, the half-life is given by:

t_1/2 = [A]₀ / 2k

For a first-order reaction, the half-life is given by:

t_1/2 = ln2 / k

For a second-order reaction, the half-life is given by:

t_1/2 = 1 / k[A]₀

These equations show that the half-life of a zero-order reaction is dependent on the initial concentration, while the half-life of a first-order reaction is independent of the initial concentration, and the half-life of a second-order reaction is inversely proportional to the initial concentration.

Graphical Analysis of Rate Data: How To Determine Rate Law

Graphical methods provide a powerful tool for analyzing rate data and determining the order of a reaction. By plotting the concentration of a reactant or product as a function of time, we can visually identify the relationship between these variables and determine the order of the reaction with respect to each reactant.

Types of Plots Used in Graphical Analysis

The type of plot used in graphical analysis depends on the order of the reaction. Here are the three main types of plots:

• Zero-order reaction: A plot of [reactant] vs. time yields a straight line with a negative slope. The rate constant (k) is equal to the negative of the slope.
• First-order reaction: A plot of ln[reactant] vs. time yields a straight line with a negative slope. The rate constant (k) is equal to the negative of the slope.
• Second-order reaction: A plot of 1/[reactant] vs. time yields a straight line with a positive slope. The rate constant (k) is equal to the slope.

Examples of Analyzing Rate Data Using Graphical Methods

Let’s illustrate how to analyze rate data using graphical methods with a hypothetical example:

Example:

Consider the reaction:

A → Products

We have collected the following data:

| Time (s) | [A] (M) |
|—|—|
| 0 | 1.00 |
| 10 | 0.75 |
| 20 | 0.56 |
| 30 | 0.42 |
| 40 | 0.31 |

Analysis:

1. Zero-order plot: Plot [A] vs. time. This plot will not yield a straight line, indicating that the reaction is not zero-order.

2. First-order plot: Plot ln[A] vs. time. This plot will yield a straight line, indicating that the reaction is first-order. The slope of the line is -k.

3. Second-order plot: Plot 1/[A] vs. time. This plot will not yield a straight line, indicating that the reaction is not second-order.

Conclusion: Based on the graphical analysis, we can conclude that the reaction is first-order with respect to A.

Temperature Dependence of Rate Laws

The rate of a chemical reaction is significantly influenced by temperature. As temperature increases, the reaction rate generally increases. This relationship between temperature and reaction rate can be explained by the Arrhenius equation.

The Arrhenius Equation

The Arrhenius equation is a mathematical expression that quantifies the relationship between the rate constant (k) of a reaction and temperature (T). It is given by:

k = A * exp(-Ea/RT)

Where:

* k is the rate constant
* A is the pre-exponential factor, which is a constant that represents the frequency of collisions between reactant molecules
* Ea is the activation energy, which is the minimum amount of energy that reactant molecules must possess to overcome the energy barrier and form products
* R is the ideal gas constant (8.314 J/mol·K)
* T is the absolute temperature in Kelvin

The Arrhenius equation is significant because it allows us to:

* Predict the rate of a reaction at a given temperature.
* Determine the activation energy of a reaction.
* Understand the effect of temperature on the rate constant.

Determining the Activation Energy

The activation energy (Ea) can be determined experimentally by measuring the rate constant at different temperatures. By taking the natural logarithm of both sides of the Arrhenius equation, we obtain a linear equation:

ln(k) = -Ea/R * (1/T) + ln(A)

This equation has the form of a straight line, y = mx + c, where:

* y = ln(k)
* x = 1/T
* m = -Ea/R
* c = ln(A)

Therefore, a plot of ln(k) versus 1/T will yield a straight line with a slope of -Ea/R. The activation energy can then be calculated from the slope of the line.

Relationship Between Temperature and Reaction Rate

The Arrhenius equation demonstrates that the rate constant (k) increases exponentially with temperature. This means that a small increase in temperature can lead to a significant increase in the reaction rate.

For example, the rate constant for a reaction might double for every 10°C increase in temperature. This is because the increased temperature provides more energy to the reactant molecules, increasing the number of collisions that have enough energy to overcome the activation energy barrier.

In general, the relationship between temperature and reaction rate can be summarized as follows:

* Higher temperature: More molecules have sufficient energy to overcome the activation energy barrier, leading to a faster reaction rate.
* Lower temperature: Fewer molecules have sufficient energy to overcome the activation energy barrier, leading to a slower reaction rate.

Catalysis and Rate Laws

Catalysts are substances that increase the rate of a chemical reaction without being consumed in the process. They achieve this by providing an alternative reaction pathway with a lower activation energy, thus allowing more molecules to overcome the energy barrier and react. The study of catalysis is crucial in understanding how reaction rates are affected by the presence of these substances.

Types of Catalysts

Catalysts can be broadly classified into two main types: homogeneous and heterogeneous catalysts.

• Homogeneous Catalysts: These catalysts exist in the same phase as the reactants. For example, in a liquid-phase reaction, a homogeneous catalyst would also be dissolved in the liquid. A classic example is the use of acids to catalyze esterification reactions, where the acid catalyst is dissolved in the same liquid phase as the alcohol and carboxylic acid reactants.
• Heterogeneous Catalysts: These catalysts exist in a different phase than the reactants. For example, a solid catalyst might be used to catalyze a gas-phase reaction. A common example is the use of a platinum catalyst in the catalytic converter of a car, where the platinum solid catalyzes the conversion of harmful gases like carbon monoxide and nitrogen oxides into less harmful products.

Effect of Catalysts on Rate Law

Catalysts do not alter the equilibrium constant of a reaction; they only affect the rate at which equilibrium is reached. This is because catalysts provide an alternative pathway with a lower activation energy, which increases the rate of both the forward and reverse reactions equally.

Catalysts can affect the rate law of a reaction in several ways:

• Changing the Rate Constant: The most common effect of a catalyst is to increase the rate constant (k) of the reaction. This is because the catalyst lowers the activation energy, leading to a faster rate of reaction at a given temperature.
• Altering the Reaction Mechanism: Catalysts can change the mechanism of a reaction by providing an alternative pathway. This can lead to different rate laws, as the mechanism dictates the order of the reaction with respect to each reactant.
• Introducing New Reactants: Some catalysts participate in the reaction mechanism and can be considered as reactants. This can lead to a different rate law, as the catalyst itself appears in the rate equation.

For example, consider the decomposition of hydrogen peroxide (H₂O₂) into water (H₂O) and oxygen (O₂). This reaction is slow at room temperature. However, in the presence of a catalyst like manganese dioxide (MnO₂), the reaction proceeds much faster. The catalyst provides an alternative pathway with a lower activation energy, leading to a faster rate of decomposition.

Wrap-Up

Determining rate laws is an essential skill in chemical kinetics, enabling us to understand the intricacies of chemical reactions. Through experimental methods like the method of initial rates and graphical analysis of rate data, we can uncover the order of a reaction, identify the rate constant, and even delve into the activation energy and the influence of temperature on reaction rates. Armed with this knowledge, we can optimize chemical processes, design more efficient catalysts, and unravel the mysteries of chemical transformations.

Popular Questions

What is the difference between a rate law and an integrated rate law?

A rate law describes the relationship between the rate of a reaction and the concentrations of reactants, while an integrated rate law relates the concentration of a reactant to time. The integrated rate law is derived from the rate law and is used to predict the concentration of a reactant at a given time.

What are the units of the rate constant?

The units of the rate constant depend on the order of the reaction. For example, the units of the rate constant for a first-order reaction are s^-1, while the units for a second-order reaction are M^-1s^-1.

How can I determine the order of a reaction experimentally?

The order of a reaction can be determined experimentally using the method of initial rates or by graphical analysis of rate data. The method of initial rates involves measuring the initial rate of the reaction at different initial concentrations of reactants. The order of the reaction is then determined by analyzing how the initial rate changes with changes in concentration.