How to find rate law sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. Understanding rate laws is fundamental in chemical kinetics, the study of reaction rates and mechanisms. It’s like having a roadmap for a chemical reaction, guiding us through the intricate pathways of molecules as they transform. By unraveling the secrets of rate laws, we gain valuable insights into how reactions proceed, allowing us to predict their speed, optimize conditions, and even design new reactions.
This journey begins with a definition of rate laws and their significance, exploring the intricate relationship between reaction rate, reactant concentrations, and the elusive rate constant. We’ll delve into experimental methods like the method of initial rates and integrated rate laws, uncovering the secrets of determining rate laws from experimental data. Along the way, we’ll encounter the concept of reaction order, which dictates the influence of reactant concentrations on the overall reaction rate. We’ll also unravel the mysteries of the rate constant, its units, and its dependence on the overall reaction order.
Introduction to Rate Laws: How To Find Rate Law
The rate law is a mathematical expression that describes the relationship between the rate of a chemical reaction and the concentrations of the reactants. It is a fundamental concept in chemical kinetics, which is the study of reaction rates and mechanisms. The rate law is essential for understanding how reactions proceed and for predicting the rate of a reaction under different conditions.
The rate law is derived experimentally and cannot be predicted from the balanced chemical equation. It provides valuable insights into the reaction mechanism, which describes the step-by-step process by which reactants are converted into products.
Relationship Between Rate Law, Rate Constant, and Reactant Concentrations
The rate law typically takes the form:
Rate = k[A]m[B]n
where:
* Rate is the speed at which the reaction proceeds, usually expressed as the change in concentration of a reactant or product per unit time.
* k is the rate constant, a proportionality constant that reflects the intrinsic rate of the reaction at a specific temperature.
* [A] and [B] are the concentrations of reactants A and B, respectively.
* m and n are the orders of the reaction with respect to reactants A and B, respectively. These exponents are determined experimentally and indicate the sensitivity of the reaction rate to changes in the concentration of each reactant.
The rate constant, k, is independent of the concentrations of reactants but is dependent on temperature and the presence of catalysts. The rate constant provides a quantitative measure of the reaction’s speed at a given temperature.
Examples of Rate Laws for Different Types of Reactions
The following are examples of rate laws for different types of reactions:
* First-order reaction: A reaction where the rate is directly proportional to the concentration of one reactant.
* Example: The decomposition of nitrogen pentoxide (N2O5)
Rate = k[N2O5]
* Second-order reaction: A reaction where the rate is proportional to the square of the concentration of one reactant or the product of the concentrations of two reactants.
* Example: The reaction between hydrogen (H2) and iodine (I2) to form hydrogen iodide (HI)
Rate = k[H2][I2]
* Zero-order reaction: A reaction where the rate is independent of the concentrations of reactants.
* Example: The decomposition of ammonia (NH3) on a hot platinum surface
Rate = k
Experimental Methods for Determining Rate Laws
Determining the rate law for a chemical reaction is crucial for understanding its kinetics and predicting its behavior under various conditions. This section will explore various experimental methods employed to determine rate laws.
Method of Initial Rates
The method of initial rates involves measuring the initial rate of a reaction at different initial concentrations of reactants. This method relies on the assumption that the initial rate is directly proportional to the initial concentrations of reactants raised to their respective orders in the rate law.
The method of initial rates involves conducting a series of experiments where the initial concentrations of reactants are varied while keeping the temperature constant. The initial rate of the reaction is then measured for each experiment. By analyzing the changes in initial rates as the initial concentrations of reactants are changed, we can determine the order of the reaction with respect to each reactant.
For example, consider the reaction:
A + B → C
To determine the rate law, we can perform a series of experiments with different initial concentrations of A and B and measure the initial rates.
| Experiment | [A] (M) | [B] (M) | Initial Rate (M/s) |
|—|—|—|—|
| 1 | 0.1 | 0.1 | 0.01 |
| 2 | 0.2 | 0.1 | 0.02 |
| 3 | 0.1 | 0.2 | 0.04 |
By analyzing the data, we can observe that doubling the concentration of A doubles the initial rate, indicating that the reaction is first order with respect to A. Similarly, doubling the concentration of B quadruples the initial rate, indicating that the reaction is second order with respect to B. Therefore, the overall rate law for this reaction is:
Rate = k[A][B]^2
where k is the rate constant.
Integrated Rate Law Method
The integrated rate law method utilizes the integrated form of the rate law, which relates the concentration of a reactant to time. This method is particularly useful when the initial rate method is not practical or when the reaction is complex and involves multiple steps.
The integrated rate law method involves measuring the concentration of a reactant at different times during the reaction. By plotting the concentration data against time, we can determine the order of the reaction and the rate constant.
For example, consider the first-order reaction:
A → Products
The integrated rate law for this reaction is:
ln[A]t – ln[A]0 = -kt
where [A]t is the concentration of A at time t, [A]0 is the initial concentration of A, and k is the rate constant.
By plotting ln[A]t against time, we obtain a straight line with a slope of -k. This allows us to determine the rate constant and confirm the first-order nature of the reaction.
Method of Isolation
The method of isolation involves studying the reaction by varying the concentration of one reactant while keeping the concentrations of all other reactants constant. This allows us to determine the order of the reaction with respect to the reactant being varied.
For example, consider the reaction:
A + B + C → Products
To determine the order of the reaction with respect to A, we can perform a series of experiments where the concentration of A is varied while keeping the concentrations of B and C constant. By analyzing the changes in the rate of the reaction as the concentration of A is changed, we can determine the order of the reaction with respect to A.
This method helps isolate the effect of one reactant on the rate of the reaction, allowing us to determine its individual contribution to the overall rate law.
Determining the Rate Constant
Once you’ve established the rate law for a reaction, the next step is to determine the rate constant, often denoted as *k*. The rate constant quantifies the reaction’s speed at a specific temperature. It is a proportionality constant that relates the rate of reaction to the concentrations of reactants.
Calculating the Rate Constant
To calculate the rate constant, you need experimental data that includes the initial concentrations of reactants and the initial rate of the reaction. The rate law provides the relationship between the rate, concentrations, and the rate constant. By substituting the experimental values into the rate law equation, you can solve for *k*.
For example, consider a reaction with the following rate law:
Rate = *k*[A]^m[B]^n
where:
– Rate is the initial rate of reaction.
– *k* is the rate constant.
– [A] and [B] are the initial concentrations of reactants A and B, respectively.
– *m* and *n* are the orders of the reaction with respect to A and B, respectively.
To calculate *k*, you need to know the values of Rate, [A], [B], *m*, and *n*. These values can be obtained from experimental data. Once you have these values, you can plug them into the rate law equation and solve for *k*.
Units of the Rate Constant
The units of the rate constant depend on the overall order of the reaction. Here’s how to determine the units:
– Overall order = 0: The units of *k* are the same as the units of the rate, typically M/s (molar per second).
– Overall order = 1: The units of *k* are s⁻¹ (per second).
– Overall order = 2: The units of *k* are M⁻¹s⁻¹ (molar inverse second).
– Overall order = n: The units of *k* are M¹⁻ⁿs⁻¹ (molar to the power of (1-n) per second).
Examples of Calculating Rate Constants
Example 1: Consider the following reaction:
2NO(g) + O₂(g) → 2NO₂(g)
The rate law for this reaction is determined to be:
Rate = *k*[NO]²[O₂]
Let’s say that in one experiment, the initial concentration of NO is 0.10 M, the initial concentration of O₂ is 0.20 M, and the initial rate of the reaction is 1.0 × 10⁻⁵ M/s.
We can calculate the rate constant (*k*) as follows:
1.0 × 10⁻⁵ M/s = *k*(0.10 M)²(0.20 M)
Solving for *k*, we get:
*k* = 5.0 × 10⁻³ M⁻²s⁻¹
Example 2: For a first-order reaction, the rate law is:
Rate = *k*[A]
Let’s say the initial concentration of A is 0.50 M and the initial rate is 2.5 × 10⁻⁴ M/s.
Plugging these values into the rate law equation:
2.5 × 10⁻⁴ M/s = *k*(0.50 M)
Solving for *k*:
*k* = 5.0 × 10⁻⁴ s⁻¹
These examples illustrate how to calculate the rate constant using experimental data and the rate law equation.
Reaction Order and Rate Law
The rate law is an equation that describes the relationship between the rate of a reaction and the concentrations of the reactants. The reaction order is a concept that helps us understand how the rate of a reaction changes with the concentration of each reactant.
The reaction order is a key concept in chemical kinetics. It tells us how the rate of a reaction changes as the concentration of each reactant changes. This information is essential for predicting the rate of a reaction under different conditions and for designing experiments to study reaction mechanisms.
Determining the Reaction Order
The reaction order with respect to each reactant can be determined experimentally. This involves measuring the initial rate of the reaction at different concentrations of each reactant while keeping the concentrations of other reactants constant.
Here’s how to determine the reaction order for a reactant:
– Step 1: Measure the initial rate of the reaction at different concentrations of the reactant.
– Step 2: Keep the concentrations of all other reactants constant.
– Step 3: Analyze the data to determine the relationship between the concentration of the reactant and the initial rate.
If the initial rate doubles when the concentration of a reactant doubles, the reaction is first order with respect to that reactant. If the initial rate quadruples when the concentration of a reactant doubles, the reaction is second order with respect to that reactant.
The reaction order with respect to a reactant is the exponent to which the concentration of that reactant is raised in the rate law.
For example, consider the following reaction:
A + B → C
The rate law for this reaction might be:
Rate = k[A]^m[B]^n
where:
– k is the rate constant
– [A] and [B] are the concentrations of reactants A and B, respectively
– m and n are the reaction orders with respect to A and B, respectively.
To determine the reaction order with respect to A, we would perform a series of experiments where we vary the concentration of A while keeping the concentration of B constant. We would then measure the initial rate of the reaction at each concentration of A. By analyzing the data, we can determine the value of m.
The same procedure can be followed to determine the reaction order with respect to B.
Overall Reaction Order
The overall reaction order is the sum of the individual reaction orders for each reactant. In the example above, the overall reaction order would be m + n.
The overall reaction order tells us how the rate of the reaction changes as the concentrations of all reactants change. For example, if the overall reaction order is 2, the rate of the reaction will quadruple if the concentrations of all reactants are doubled.
The overall reaction order is related to the rate constant (k) in the following way:
The rate constant is a proportionality constant that relates the rate of a reaction to the concentrations of the reactants.
The units of the rate constant depend on the overall reaction order. For a first-order reaction, the units of the rate constant are s-1. For a second-order reaction, the units of the rate constant are M-1s-1.
The rate constant is a valuable tool for understanding the kinetics of a reaction. It can be used to predict the rate of a reaction under different conditions, and it can be used to study the mechanism of a reaction.
Examples and Applications
Rate laws are not merely theoretical constructs; they have significant practical applications in various fields, from chemistry and biology to engineering and environmental science. Understanding the rate law of a reaction allows us to predict how fast a reaction will proceed under different conditions and to optimize reaction conditions for maximum efficiency.
Real-World Examples of Rate Laws
Rate laws are crucial for understanding and predicting the behavior of chemical reactions. Here are some real-world examples:
- Combustion: The burning of fuels, a fundamental process in power generation and transportation, involves complex reactions with rate laws that determine the rate of heat release and the efficiency of combustion. For instance, the rate of combustion of methane (CH4) in air is influenced by factors like temperature, oxygen concentration, and the presence of catalysts.
- Atmospheric Chemistry: The formation and destruction of ozone (O3) in the stratosphere is governed by rate laws. Understanding these rate laws is essential for modeling the ozone layer and assessing the impact of pollutants on its depletion.
- Enzyme Kinetics: Enzymes are biological catalysts that accelerate biochemical reactions in living organisms. The rate of enzyme-catalyzed reactions is often described by the Michaelis-Menten equation, a specific form of a rate law that takes into account the enzyme concentration and substrate concentration.
Applications of Rate Laws in Predicting Reaction Rates and Optimizing Reaction Conditions
Rate laws provide a powerful tool for predicting reaction rates and optimizing reaction conditions.
- Predicting Reaction Rates: Once the rate law for a reaction is determined, we can predict how the reaction rate will change under different conditions, such as varying temperature, reactant concentrations, or the presence of catalysts. This information is valuable for designing and controlling chemical processes.
- Optimizing Reaction Conditions: Rate laws can be used to determine the optimal conditions for a reaction to proceed at the desired rate. For example, by understanding the rate law for a particular reaction, we can determine the ideal temperature, pressure, and reactant concentrations to maximize product yield and minimize side reactions.
Examples of Rate Laws in Industrial Processes and Research
Rate laws play a critical role in numerous industrial processes and research endeavors:
- Chemical Synthesis: In the chemical industry, rate laws are essential for optimizing the synthesis of various products, such as pharmaceuticals, polymers, and fertilizers. By understanding the rate law of a particular reaction, chemists can control the reaction conditions to achieve the desired product yield and purity.
- Environmental Remediation: Rate laws are used to study the degradation of pollutants in the environment. For example, understanding the rate law for the degradation of pesticides in soil can help researchers predict their persistence and develop strategies for their removal.
- Materials Science: Rate laws are employed in materials science to study the kinetics of material formation and degradation. This knowledge is crucial for developing new materials with desired properties and for predicting their lifetime under various conditions.
Factors Affecting Rate Laws
The rate of a chemical reaction can be influenced by various factors, including temperature, the presence of catalysts, and the surface area of reactants in heterogeneous reactions. Understanding these factors is crucial for controlling and predicting reaction rates.
Temperature’s Impact on Reaction Rates
Temperature plays a significant role in determining the rate of a chemical reaction. As temperature increases, the average kinetic energy of molecules increases, leading to more frequent and energetic collisions. This increased collision frequency and energy enhance the likelihood of successful collisions, resulting in a faster reaction rate.
The relationship between temperature and reaction rate is described by the Arrhenius equation, which provides a quantitative framework for understanding this dependence.
The Arrhenius equation: k = A * exp(-Ea/RT)
where:
* k is the rate constant
* A is the pre-exponential factor, representing the frequency of collisions
* Ea is the activation energy, the minimum energy required for a reaction to occur
* R is the ideal gas constant
* T is the absolute temperature
The Arrhenius equation shows that the rate constant, and consequently the reaction rate, increases exponentially with temperature. This exponential dependence highlights the significant impact of temperature on reaction rates.
Effect of Catalysts on Reaction Rates
Catalysts are substances that accelerate the rate of a chemical reaction without being consumed in the process. They achieve this by providing an alternative reaction pathway with a lower activation energy. This lowered activation energy allows more molecules to overcome the energy barrier, leading to a faster reaction rate.
Catalysts work by forming temporary intermediates with reactants, facilitating the formation of products. These intermediates have a lower activation energy than the original reactants, thus accelerating the reaction.
For example, the decomposition of hydrogen peroxide (H2O2) is significantly accelerated by the presence of a catalyst like manganese dioxide (MnO2). The catalyst provides an alternative pathway for the decomposition, lowering the activation energy and increasing the reaction rate.
Influence of Surface Area on Reaction Rates
For heterogeneous reactions, where reactants are in different phases (e.g., solid-liquid or gas-solid), the surface area of the solid reactant significantly affects the reaction rate.
In heterogeneous reactions, the reaction occurs at the interface between the phases. Increasing the surface area of the solid reactant provides more contact points for the reaction to occur, leading to a faster reaction rate.
For instance, the combustion of wood is faster when the wood is in the form of sawdust compared to a large log. This is because sawdust has a much larger surface area, providing more contact points for oxygen to react with the wood, leading to a faster combustion rate.
Complex Reactions and Rate Laws
Many chemical reactions occur in a series of steps, rather than a single step. These multi-step reactions are called complex reactions, and understanding their mechanisms is crucial for predicting and controlling their rates.
The individual steps in a complex reaction are called elementary steps, and each step represents a single molecular event. The overall reaction mechanism is the sequence of elementary steps that leads from reactants to products.
Elementary Steps and Reaction Mechanisms, How to find rate law
The rate law for an elementary step can be determined directly from its stoichiometry. The order of the reaction with respect to each reactant is equal to its stoichiometric coefficient in the balanced elementary step.
For example, consider the following elementary step:
A + B → C
The rate law for this step would be:
Rate = k[A][B]
where k is the rate constant.
The overall rate law for a complex reaction is determined by the slowest step in the mechanism, known as the rate-determining step. This step limits the overall rate of the reaction, and its rate law governs the overall rate law.
Deriving the Rate Law for a Complex Reaction
To derive the rate law for a complex reaction, we need to identify the rate-determining step and then use its rate law to determine the overall rate law.
Here’s a step-by-step process:
1. Write the balanced chemical equation for the overall reaction.
2. Propose a mechanism, a sequence of elementary steps that leads from reactants to products.
3. Identify the rate-determining step. This is usually the slowest step in the mechanism.
4. Write the rate law for the rate-determining step.
5. Use the rate law for the rate-determining step to determine the overall rate law. This may involve substituting for intermediate species that appear in the rate law.
Examples of Complex Reactions and Their Rate Laws
Here are a few examples of complex reactions and their corresponding rate laws:
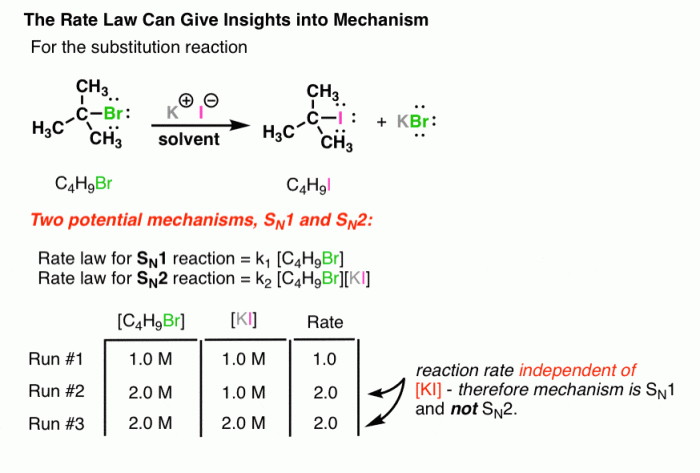
1. The Decomposition of Ozone:
The decomposition of ozone (O3) into oxygen (O2) occurs in two steps:
* Step 1: O3 → O2 + O (slow)
* Step 2: O + O3 → 2O2 (fast)
The rate-determining step is the first step, and its rate law is:
Rate = k[O3]
The overall rate law is the same as the rate law for the rate-determining step:
Rate = k[O3]
2. The Reaction of Hydrogen and Iodine:
The reaction of hydrogen (H2) and iodine (I2) to form hydrogen iodide (HI) occurs in two steps:
* Step 1: I2 → 2I (fast)
* Step 2: 2I + H2 → 2HI (slow)
The rate-determining step is the second step, and its rate law is:
Rate = k[I]^2[H2]
Since the first step is fast, we can assume that the concentration of iodine atoms (I) is in equilibrium with the concentration of iodine molecules (I2). Using the equilibrium constant for the first step, we can substitute for [I] in the rate law for the second step, resulting in the overall rate law:
Rate = k'[I2][H2]
where k’ is a new rate constant that incorporates the equilibrium constant for the first step.
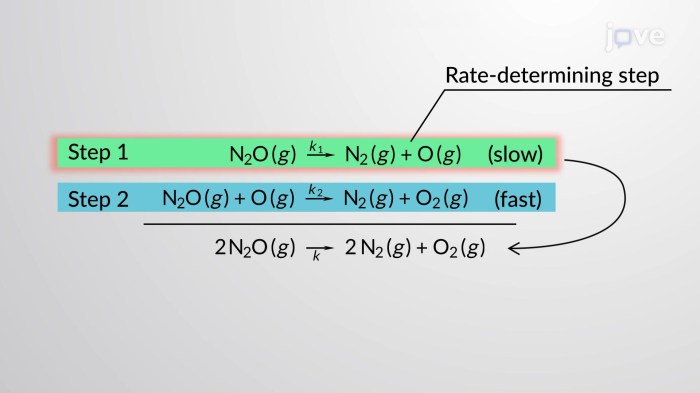
3. The SN1 Reaction:
The SN1 reaction is a unimolecular nucleophilic substitution reaction that proceeds in two steps:
* Step 1: R-X → R+ + X- (slow)
* Step 2: R+ + Nu- → R-Nu (fast)
The rate-determining step is the first step, and its rate law is:
Rate = k[R-X]
The overall rate law is the same as the rate law for the rate-determining step:
Rate = k[R-X]
Final Summary

Armed with this knowledge, we can confidently navigate the world of chemical kinetics, predicting reaction rates, optimizing reaction conditions, and even designing new reactions. Whether you’re a student embarking on a journey of chemical discovery or a seasoned researcher pushing the boundaries of scientific knowledge, understanding rate laws is a crucial stepping stone to success. So, let’s embark on this captivating exploration of how to find rate law and unlock the secrets of chemical reactions.
FAQs
What is the difference between a rate law and an integrated rate law?
A rate law expresses the relationship between the rate of a reaction and the concentrations of reactants. An integrated rate law relates the concentration of a reactant to time. The integrated rate law is derived from the rate law by integration.
How do catalysts affect rate laws?
Catalysts speed up reactions without being consumed in the process. They do not affect the equilibrium position of a reaction, but they change the mechanism of the reaction, providing an alternative pathway with a lower activation energy. This means the rate constant will be higher in the presence of a catalyst, but the overall reaction order remains the same.
What are some common applications of rate laws in real-world scenarios?
Rate laws are essential in many industrial processes, such as designing efficient chemical reactors, optimizing reaction conditions for maximum yield, and understanding the degradation of materials over time. They are also used in environmental studies to predict the fate of pollutants and in medicine to study the metabolism of drugs.





