What is Hooke’s Law? It’s a fundamental principle in physics that explains the behavior of elastic materials when subjected to forces. Discovered by Robert Hooke in the 17th century, this law describes the relationship between the force applied to a spring-like object and the resulting displacement. Imagine stretching a rubber band; the further you pull, the greater the force required to stretch it. Hooke’s Law quantifies this relationship, providing a simple yet powerful tool to understand the elasticity of materials in various applications.
Hooke’s Law is not just a theoretical concept; it has practical implications in everyday life. From the springs in your car’s suspension system to the elasticity of your muscles, Hooke’s Law governs the behavior of these systems. It plays a crucial role in engineering, physics, and even biology, helping us design structures, predict the motion of objects, and understand the mechanics of living organisms.
Mathematical Formulation of Hooke’s Law
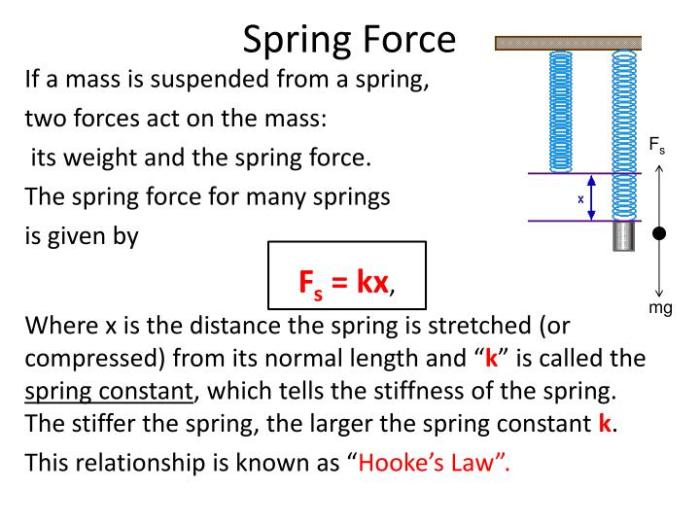
Hooke’s Law, a fundamental principle in physics, provides a quantitative relationship between the force applied to an elastic object and the resulting deformation. It states that the force required to stretch or compress a spring is directly proportional to the displacement from its equilibrium position. This relationship can be expressed mathematically, providing a powerful tool for understanding and predicting the behavior of elastic materials.
The Equation of Hooke’s Law
Hooke’s Law is mathematically represented by the following equation:
F = -kx
where:
- F represents the force applied to the spring, measured in Newtons (N).
- x represents the displacement of the spring from its equilibrium position, measured in meters (m).
- k represents the spring constant, measured in Newtons per meter (N/m).
The negative sign in the equation indicates that the force exerted by the spring is always in the opposite direction to the displacement. For example, if the spring is stretched, the force will act to pull it back towards its equilibrium position.
Significance of the Spring Constant (k)
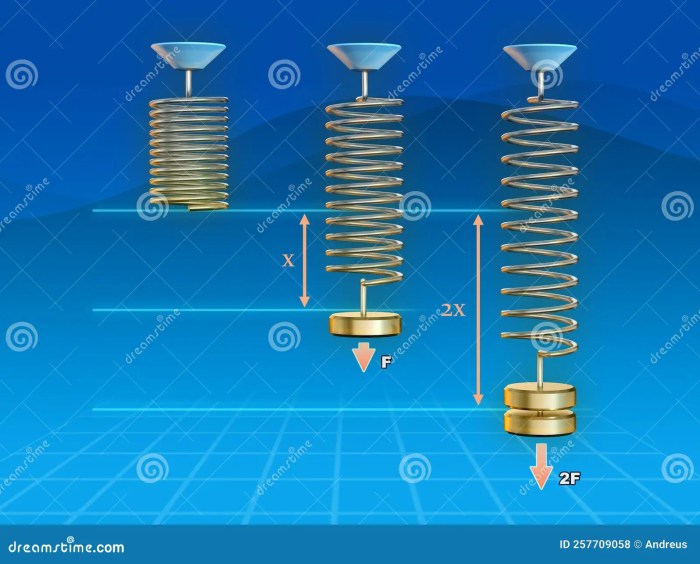
The spring constant (k) is a crucial parameter in Hooke’s Law, as it quantifies the stiffness of the spring. A higher spring constant indicates a stiffer spring, requiring a greater force to produce a given displacement. Conversely, a lower spring constant represents a more flexible spring, which can be stretched or compressed more easily.
The value of the spring constant depends on several factors, including:
- Material properties: The material from which the spring is made significantly influences its stiffness. For instance, a steel spring will generally have a higher spring constant than a rubber spring of the same dimensions.
- Geometry: The shape and dimensions of the spring also play a role. A thicker spring will typically have a higher spring constant than a thinner spring of the same material.
- Temperature: The temperature of the spring can affect its stiffness. In general, an increase in temperature will lead to a decrease in stiffness, resulting in a lower spring constant.
Proportionality and Linear Relationship
The key concept underlying Hooke’s Law is proportionality. This means that the force applied to the spring is directly proportional to the displacement. This linear relationship holds true only within the elastic limit of the material.
The elastic limit refers to the maximum stress or strain that a material can withstand before undergoing permanent deformation. Within this limit, the material will return to its original shape after the force is removed. Beyond the elastic limit, the material will exhibit plastic deformation, and Hooke’s Law no longer applies.
For example, if you stretch a spring beyond its elastic limit, it will not return to its original length when the force is released. Instead, it will remain permanently deformed. This illustrates the importance of considering the elastic limit when applying Hooke’s Law.
Applications of Hooke’s Law

Hooke’s Law, a fundamental principle in physics, finds extensive applications in various fields, shaping our understanding of elasticity and its implications in numerous real-world scenarios.
Engineering Applications, What is hooke’s law
Hooke’s Law plays a crucial role in engineering, particularly in the design and analysis of structures, machines, and systems that rely on elastic materials.
Bridges
Hooke’s Law is fundamental in bridge design, as it helps engineers determine the load-bearing capacity of bridge components. The principle of elasticity dictates how much a bridge can deform under stress without permanent damage.
The deflection of a bridge beam under a load is directly proportional to the load and inversely proportional to the stiffness of the beam, as defined by Hooke’s Law.
Buildings
Similar to bridges, buildings also rely heavily on Hooke’s Law for structural integrity. Engineers use this law to calculate the stress and strain on building materials, ensuring that structures can withstand various loads and environmental conditions.
The strength of building materials, like steel and concrete, is determined by their elastic properties, which are governed by Hooke’s Law.
Suspension Systems
Hooke’s Law is essential in the design of suspension systems for vehicles, where springs are used to absorb shocks and vibrations. By understanding the relationship between force and displacement in springs, engineers can optimize the performance and comfort of vehicles.
The spring constant, a measure of a spring’s stiffness, is directly related to the force required to compress or extend the spring, as described by Hooke’s Law.
Physics Applications
Hooke’s Law is a cornerstone of many concepts in physics, particularly in the study of oscillations and simple harmonic motion.
Simple Harmonic Motion
Hooke’s Law forms the basis of simple harmonic motion, a fundamental type of periodic motion where the restoring force is directly proportional to the displacement from equilibrium.
The equation for simple harmonic motion, which describes the oscillatory behavior of a mass attached to a spring, is derived directly from Hooke’s Law.
Oscillations
Hooke’s Law is applicable to various oscillating systems, including pendulums, springs, and even sound waves. By understanding the elastic properties of materials, physicists can predict and analyze the frequency and amplitude of oscillations.
The period of oscillation of a simple pendulum, for example, is directly related to the length of the pendulum and the acceleration due to gravity, which can be derived using Hooke’s Law.
Biology Applications
Hooke’s Law finds applications in biology, particularly in understanding the elastic properties of biological materials and structures.
Muscle Elasticity
Hooke’s Law is used to study the elasticity of muscles, which are responsible for movement and force generation in the body. Understanding the elastic properties of muscles is crucial for understanding their function and how they respond to various stimuli.
The force generated by a muscle is directly proportional to the amount of stretch or contraction, as defined by Hooke’s Law.
Cell Mechanics
Hooke’s Law is applied to study the mechanical properties of cells, which are essential for cell division, migration, and other biological processes. By understanding the elasticity of cell membranes and cytoskeletons, researchers can gain insights into cellular function and disease mechanisms.
The stiffness of cells, which is related to their ability to resist deformation, is governed by the elastic properties of their constituent components, as described by Hooke’s Law.
| Field | Applications | Examples |
|---|---|---|
| Engineering | Design of bridges, buildings, suspension systems | – Calculation of load-bearing capacity of bridge components – Determination of stress and strain on building materials – Optimization of spring stiffness in vehicle suspension systems |
| Physics | Simple harmonic motion, oscillations | – Analysis of the motion of a mass attached to a spring – Prediction of the frequency and amplitude of oscillations in various systems |
| Biology | Muscle elasticity, cell mechanics | – Study of the force-generating capacity of muscles – Understanding the stiffness and deformability of cells |
Wrap-Up
Hooke’s Law, while a simple concept, provides a powerful framework for understanding the behavior of elastic materials. Its applications are vast, ranging from engineering structures to the workings of our own bodies. While it has limitations, especially when dealing with materials beyond their elastic limit, Hooke’s Law remains a cornerstone of physics, offering valuable insights into the world around us.
Clarifying Questions: What Is Hooke’s Law
What is the elastic limit?
The elastic limit is the maximum stress a material can withstand before it permanently deforms. Beyond this limit, the material will not return to its original shape after the force is removed.
How is Hooke’s Law used in engineering?
Hooke’s Law is crucial in engineering for designing structures like bridges, buildings, and suspension systems. It helps engineers calculate the forces and stresses materials will experience and ensure their stability.
What are some examples of real-world applications of Hooke’s Law?
Examples include springs in a car suspension system, the elasticity of a rubber band, and the bending of a diving board.





