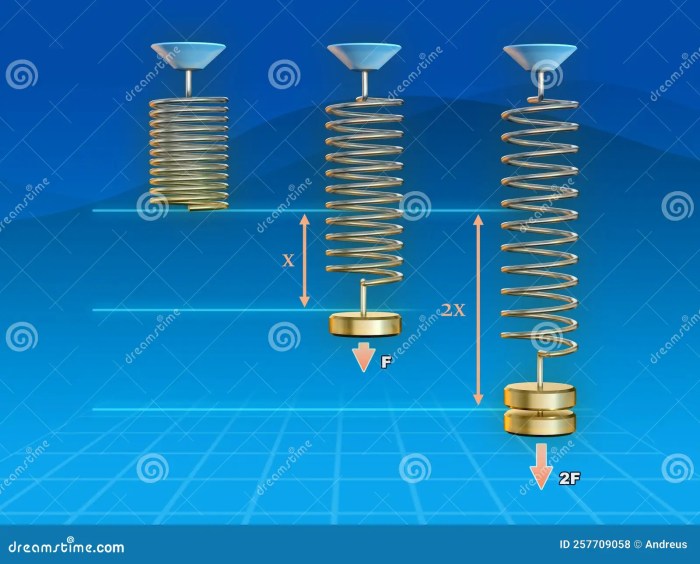
What is the hooke’s law – What is Hooke’s Law? This fundamental principle in physics describes the relationship between the force applied to a spring and the resulting displacement. Discovered by Robert Hooke in the 17th century, this law has become a cornerstone of understanding elasticity and its applications in various fields.
Hooke’s Law states that the force required to stretch or compress a spring is directly proportional to the displacement from its equilibrium position. Mathematically, this is represented by the equation F = -kx, where F is the force, x is the displacement, and k is the spring constant, which is a measure of the stiffness of the spring. This simple equation holds the key to understanding the behavior of springs and other elastic materials, from the springs in our everyday objects to the intricate structures of bridges and buildings.
Introduction to Hooke’s Law
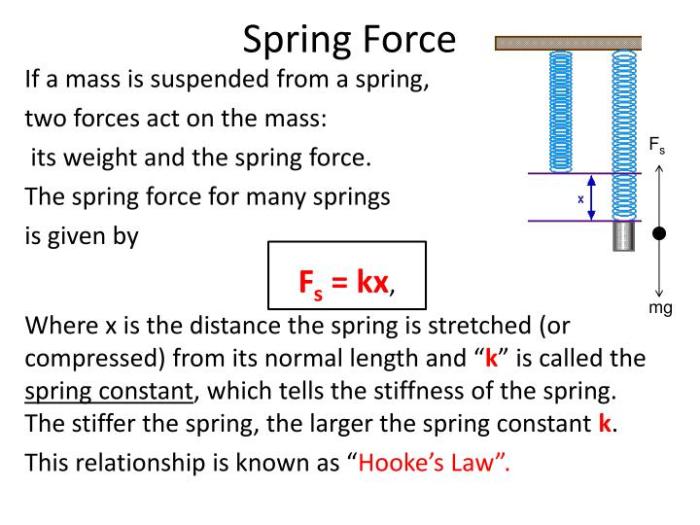
Hooke’s Law, a fundamental principle in physics, describes the relationship between the force applied to a spring and its resulting deformation. This law, formulated by English scientist Robert Hooke in 1660, has profound implications for understanding the behavior of elastic materials and plays a crucial role in various fields, including engineering, mechanics, and material science.
Hooke’s Law states that the force required to extend or compress a spring is directly proportional to the displacement from its equilibrium position. This means that the greater the force applied, the greater the deformation.
Mathematical Expression of Hooke’s Law
The mathematical expression of Hooke’s Law is:
F = -kx
where:
* F represents the force applied to the spring.
* k is the spring constant, a measure of the spring’s stiffness.
* x is the displacement of the spring from its equilibrium position.
The negative sign indicates that the force exerted by the spring is always in the opposite direction to the displacement. This means that if the spring is stretched, the force acts to pull it back to its original position, and if it is compressed, the force acts to push it back to its original position.
Key Terms in Hooke’s Law, What is the hooke’s law
Hooke’s Law involves several key terms:
* Force: The force applied to the spring, measured in Newtons (N).
* Displacement: The change in the spring’s length from its equilibrium position, measured in meters (m).
* Spring Constant: A measure of the spring’s stiffness, represented by the symbol ‘k’ and measured in Newtons per meter (N/m). A higher spring constant indicates a stiffer spring.
* Proportionality: Hooke’s Law states that the force and displacement are directly proportional, meaning that if one quantity is doubled, the other quantity will also double.
Applications of Hooke’s Law
Hooke’s Law, a fundamental principle in physics, has wide-ranging applications in various fields. It describes the relationship between the force applied to an elastic object and the resulting deformation. This law governs the behavior of springs, elastic materials, and shock absorbers, making it crucial in engineering, physics, and material science.
Applications in Engineering
Hooke’s Law plays a vital role in engineering, particularly in structural design, mechanical systems, and material science. It helps engineers predict the behavior of materials under stress and design structures that can withstand applied forces.
Spring Applications
Springs are ubiquitous in everyday life, from simple toys to complex machinery. Their ability to store and release mechanical energy is based on Hooke’s Law. Here’s a table highlighting various types of springs and their respective applications:
| Type of Spring | Application |
|---|---|
| Helical Spring | Used in suspension systems of vehicles, door closers, and mechanical clocks. |
| Torsion Spring | Used in garage door openers, spring-loaded mechanisms, and tensioning devices. |
| Leaf Spring | Used in heavy-duty vehicles, suspension systems, and railway tracks. |
| Coil Spring | Used in shock absorbers, mattress springs, and industrial machinery. |
Elastic Materials
Hooke’s Law governs the behavior of elastic materials, which can deform under stress and return to their original shape when the stress is removed. Examples include rubber bands, steel cables, and springs. Engineers use Hooke’s Law to calculate the stress and strain on these materials, ensuring they can withstand the required loads.
Shock Absorbers
Shock absorbers are essential components in vehicles, mitigating the impact of bumps and vibrations. They work based on Hooke’s Law, utilizing springs and dampers to absorb energy and reduce oscillations. Hooke’s Law helps engineers design shock absorbers that provide optimal damping and comfort.
Applications in Physics
Hooke’s Law is a fundamental concept in physics, providing insights into the elastic properties of materials. It is used to study the behavior of solids under stress, calculate the potential energy stored in springs, and analyze the oscillations of simple harmonic motion.
Applications in Material Science
Material scientists utilize Hooke’s Law to study the mechanical properties of materials, including their elasticity, stiffness, and yield strength. This knowledge is crucial for developing new materials with desired properties for specific applications, such as aerospace, automotive, and construction industries.
Derivation of Hooke’s Law

Hooke’s Law, a fundamental principle in physics, describes the relationship between the force applied to a spring and the resulting displacement. The derivation of this law involves a simple yet elegant experiment that reveals the linear proportionality between force and displacement within the elastic limit of the spring.
Experimental Procedure
To derive Hooke’s Law, a series of measurements are taken using a spring and weights. The experimental setup consists of a spring attached to a fixed point, with weights gradually added to the other end of the spring. As each weight is added, the resulting displacement of the spring is measured.
The experimental procedure involves measuring the displacement of the spring for different applied forces.
- A spring is suspended vertically from a fixed point.
- A set of known masses is prepared.
- The initial length of the spring is measured and recorded.
- The first mass is attached to the spring, and the new length is measured.
- The difference between the initial and final lengths gives the displacement of the spring.
- The process is repeated for each mass, recording the corresponding displacement.
Force-Displacement Graph and Area
The collected data points are then plotted on a graph, with force on the y-axis and displacement on the x-axis. This graph is known as a force-displacement graph. The area under the force-displacement graph represents the work done by the force in stretching the spring.
The area under the force-displacement graph represents the work done by the force in stretching the spring.
- The force-displacement graph is typically linear, indicating a direct proportionality between force and displacement within the elastic limit of the spring.
- The slope of this linear portion of the graph represents the spring constant, which is a measure of the spring’s stiffness.
- The area under the force-displacement graph represents the work done by the force in stretching the spring. This work is stored as potential energy in the spring.
Visual Representation
The experimental setup can be visualized as follows:
[Visual representation of the experimental setup, including a spring attached to a fixed point, weights hanging from the spring, and a ruler to measure displacement.]
The data collected from the experiment can be represented in a table:
[Table showing the applied force and corresponding displacement for each weight.]
The force-displacement graph can be plotted using the data from the table. This graph will typically show a linear relationship between force and displacement, with the slope of the line representing the spring constant.
[Force-displacement graph with force on the y-axis and displacement on the x-axis. The graph should show a linear relationship between force and displacement, with the slope of the line representing the spring constant.]
Limitations of Hooke’s Law
Hooke’s Law, a fundamental principle in physics, describes the linear relationship between the force applied to a spring and its extension. However, this law has limitations and only holds true under specific conditions.
While Hooke’s Law is a valuable tool for understanding the behavior of elastic materials, it’s crucial to recognize its limitations. Understanding these limitations allows for a more comprehensive understanding of material behavior under stress and strain.
Elastic Limit
The elastic limit represents the maximum stress a material can withstand before it undergoes permanent deformation. When a force is applied to an elastic material, it stretches or compresses, and upon removal of the force, it returns to its original shape. However, exceeding the elastic limit leads to permanent deformation, and the material will not fully recover its original shape. This is because the internal structure of the material has been altered.
The elastic limit is a crucial concept in understanding the limitations of Hooke’s Law. Hooke’s Law only holds true within the elastic limit. Beyond this point, the material’s behavior becomes nonlinear, and Hooke’s Law no longer accurately predicts its response to applied forces.
Material Behavior Beyond the Elastic Limit
When a material is stretched beyond its elastic limit, it enters a region of plastic deformation. In this region, the material undergoes permanent changes in its shape. The material may exhibit yielding, where it deforms significantly under a relatively constant stress. Further stretching can lead to strain hardening, where the material becomes stronger and harder to deform.
Beyond the yield point, the material continues to deform plastically until it reaches its ultimate tensile strength, the maximum stress it can withstand before it starts to fracture. At this point, the material begins to neck down, meaning it becomes thinner at a specific point. Eventually, the material fractures, breaking apart due to the applied stress exceeding its strength.
- Plastic deformation: The material undergoes permanent changes in shape, and it will not return to its original configuration upon removal of the applied force.
- Fracture: The material breaks apart due to the applied stress exceeding its strength.
Beyond Hooke’s Law: What Is The Hooke’s Law
While Hooke’s Law provides a fundamental understanding of elastic behavior in many materials, it’s important to recognize that it’s not universally applicable. Some materials exhibit non-linear elastic behavior, deviating from the linear relationship between stress and strain. This section explores the limitations of Hooke’s Law and introduces concepts beyond its scope.
Non-Linear Elastic Behavior
Many materials, particularly those subjected to high stress levels, exhibit non-linear elastic behavior. In these cases, the stress-strain relationship is not linear, and Hooke’s Law no longer accurately predicts material response. This non-linearity can be observed in various materials, including:
- Rubber: Rubber exhibits highly non-linear elastic behavior, with its stiffness increasing significantly as the applied stress increases. This is due to the unique molecular structure of rubber, where long polymer chains are cross-linked, allowing for significant stretching and deformation. As the stress increases, these chains become more aligned, leading to increased stiffness. This behavior is particularly important in applications like tires and rubber bands, where large deformations are expected.
- Metals: While many metals exhibit linear elastic behavior within a certain stress range, they can deviate from Hooke’s Law at higher stress levels. This deviation is often attributed to the onset of plastic deformation, where permanent changes in the material’s structure occur. Examples include steel, aluminum, and copper, which can exhibit non-linear elastic behavior under high loads.
- Concrete: Concrete is a brittle material and generally does not exhibit significant elastic behavior. However, under low stress levels, it can show a slightly non-linear elastic response. This non-linearity is attributed to the complex microstructure of concrete, which involves a combination of cement paste, aggregates, and voids. The behavior of concrete under stress is highly dependent on factors like the mix design, curing conditions, and age of the material.
Stress and Strain
Stress and strain are fundamental concepts in material science, crucial for understanding material behavior under load. Stress represents the force applied per unit area, while strain represents the deformation of the material in response to the applied force.
Stress (σ) = Force (F) / Area (A)
Strain (ε) = Change in length (ΔL) / Original length (L)
Hooke’s Law establishes a direct relationship between stress and strain within the elastic limit, where the material returns to its original shape after the load is removed. This relationship is expressed as:
σ = Eε
where E is the Young’s modulus, a material property representing its stiffness or resistance to deformation.
Young’s Modulus
Young’s modulus (E) is a crucial material property that quantifies the stiffness of a material. It represents the ratio of stress to strain in the elastic region of material behavior. A higher Young’s modulus indicates a stiffer material, requiring a greater force to cause a given deformation.
E = σ / ε
Young’s modulus is an important parameter in various engineering applications, particularly in structural design, where it is used to predict the behavior of materials under load. It also plays a crucial role in determining the suitability of materials for specific applications, such as choosing the appropriate material for a bridge or a building.
Final Summary
Hooke’s Law provides a fundamental framework for understanding the behavior of elastic materials, guiding our understanding of how springs, rubber bands, and other materials respond to forces. Its applications extend beyond simple springs, influencing the design of structures, the development of shock absorbers, and even the analysis of materials at the molecular level. While there are limitations to its application, Hooke’s Law remains a vital tool in various scientific and engineering disciplines, offering a powerful insight into the world of elasticity.
Essential FAQs
What are some real-world examples of Hooke’s Law in action?
Besides springs, Hooke’s Law applies to various elastic materials like rubber bands, bungee cords, and even the stretching of a guitar string. It also plays a crucial role in shock absorbers, helping to dampen vibrations and provide a smoother ride in vehicles.
How does the spring constant affect the behavior of a spring?
A higher spring constant indicates a stiffer spring, meaning it requires more force to stretch or compress it. Conversely, a lower spring constant represents a more flexible spring that can be stretched or compressed more easily.
What happens when a material is stretched beyond its elastic limit?
Beyond the elastic limit, the material enters a region of plastic deformation, where it permanently changes shape. If the force continues to increase, the material may eventually fracture.





