What is the R in the Ideal Gas Law?

What is the r in the ideal gas law – What is the ‘R’ in the Ideal Gas Law? This fundamental constant plays a crucial role in describing the behavior of gases, acting as a bridge between pressure, volume, temperature, and the number of moles of a gas. The ideal gas law, a simplified model for gas behavior, provides a powerful tool for understanding and predicting gas properties in various applications.

The ideal gas law equation, PV = nRT, encapsulates the relationship between these variables. ‘R’, known as the ideal gas constant, represents the proportionality constant linking the product of pressure and volume to the product of the number of moles and temperature. Understanding the value and units of ‘R’ is essential for applying the ideal gas law effectively.

Introduction to the Ideal Gas Law

The ideal gas law is a fundamental equation in chemistry and physics that describes the behavior of gases under ideal conditions. It establishes a relationship between pressure, volume, temperature, and the number of moles of a gas. This law is widely used to predict and explain the behavior of gases in various applications, from industrial processes to everyday phenomena.

The ideal gas law is based on the kinetic molecular theory, which describes the behavior of gases at the molecular level. The theory postulates that gas molecules are in constant random motion, and their collisions are perfectly elastic. This means that no energy is lost during collisions, and the molecules behave as if they are point masses with no volume.

Assumptions of the Ideal Gas Law, What is the r in the ideal gas law

The ideal gas law is a theoretical model that makes several simplifying assumptions about the behavior of gases. These assumptions are:

• Gas molecules have negligible volume: The ideal gas law assumes that the volume occupied by the gas molecules themselves is negligible compared to the volume of the container. This assumption is valid at low pressures and high temperatures, where the molecules are far apart and their volume is insignificant.
• Gas molecules do not interact with each other: The ideal gas law assumes that there are no attractive or repulsive forces between gas molecules. This assumption is valid at low pressures and high temperatures, where the molecules are far apart and their interactions are negligible.
• Collisions between gas molecules are perfectly elastic: The ideal gas law assumes that collisions between gas molecules are perfectly elastic, meaning that no energy is lost during collisions. This assumption is valid at low pressures and high temperatures, where the molecules are moving fast and their collisions are short-lived.

It’s important to note that these assumptions are not always met in real-world scenarios. At high pressures and low temperatures, the volume of the gas molecules becomes significant, and intermolecular forces become important. In these cases, the ideal gas law may not accurately predict the behavior of the gas.

The Ideal Gas Law Equation

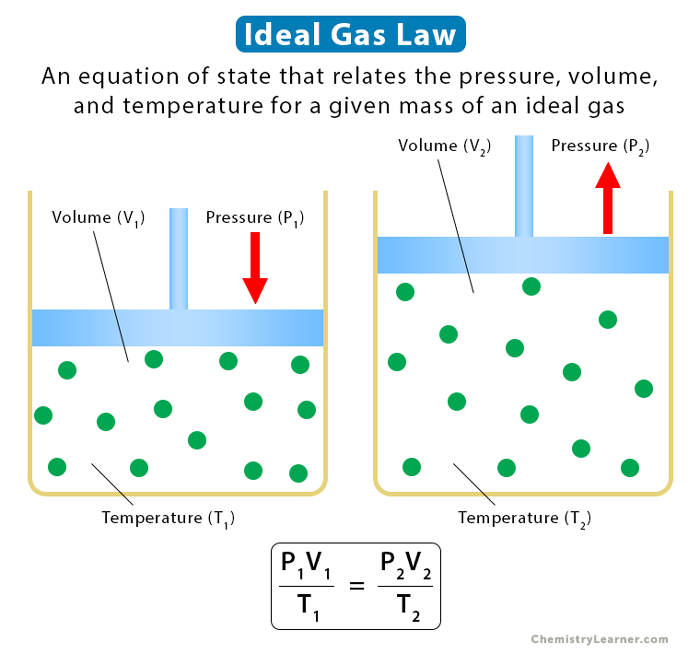
The ideal gas law is a fundamental equation in chemistry and physics that describes the behavior of ideal gases. It establishes a relationship between pressure, volume, temperature, and the amount of gas present.

The ideal gas law equation provides a concise mathematical expression for this relationship.

The Ideal Gas Law Equation

The ideal gas law is represented by the following equation:

PV = nRT

Where:

* P represents the pressure of the gas, typically measured in atmospheres (atm) or Pascals (Pa).
* V represents the volume of the gas, usually expressed in liters (L) or cubic meters (m³).
* n represents the amount of gas present, measured in moles (mol).
* R is the ideal gas constant, a proportionality constant that relates the units of measurement used for pressure, volume, temperature, and amount of substance. The value of R depends on the units used for the other variables, and its common values are:
* 0.0821 L·atm/mol·K (when pressure is in atmospheres and volume in liters)
* 8.314 J/mol·K (when pressure is in Pascals and volume in cubic meters)
* T represents the absolute temperature of the gas, measured in Kelvin (K).

Relationship Between Variables

The ideal gas law equation reveals several important relationships between the variables:

* Direct Proportionality: Pressure, volume, and temperature are directly proportional to each other. This means that if one variable increases, the other variables will also increase proportionally, assuming the remaining variables are kept constant. For example, if the temperature of a gas increases while the pressure and amount of gas remain constant, the volume of the gas will increase proportionally.
* Inverse Proportionality: Pressure and volume are inversely proportional to each other. This means that if the pressure of a gas increases, the volume of the gas will decrease proportionally, assuming the temperature and amount of gas remain constant. For example, if the pressure of a gas is doubled, the volume of the gas will be halved.

The Significance of “R” in the Ideal Gas Law

The ideal gas law, a fundamental equation in chemistry and physics, describes the relationship between pressure, volume, temperature, and the amount of an ideal gas. A crucial component of this law is the ideal gas constant, represented by the symbol “R.” This constant plays a vital role in connecting these variables and ensuring the consistency of the law across different scenarios.

The Role of “R” as the Ideal Gas Constant

The ideal gas constant, “R,” is a proportionality factor that bridges the relationship between the pressure, volume, temperature, and the amount of an ideal gas. It represents the amount of energy required to raise the temperature of one mole of an ideal gas by one degree Kelvin at constant pressure. This constant is essential for converting between different units of measurement and ensuring the validity of the ideal gas law across various conditions.

Different Units of “R” and Their Implications

The value of “R” varies depending on the units used for pressure, volume, and temperature. This variation is due to the different scales and conventions used in measuring these quantities. Some common units for “R” are:

• L·atm/mol·K: This unit is frequently used when pressure is expressed in atmospheres (atm), volume in liters (L), and temperature in Kelvin (K). The value of “R” in this unit is 0.0821 L·atm/mol·K.
• J/mol·K: This unit is used when pressure is expressed in Pascals (Pa), volume in cubic meters (m³), and temperature in Kelvin (K). The value of “R” in this unit is 8.314 J/mol·K.
• cal/mol·K: This unit is used when pressure is expressed in atmospheres (atm), volume in liters (L), and temperature in Kelvin (K). The value of “R” in this unit is 1.987 cal/mol·K.

It is crucial to choose the correct value of “R” based on the units used in the problem. Using the wrong unit can lead to incorrect results.

Examples of “R” in Calculations

The ideal gas constant, “R,” is used in various calculations involving ideal gases. Here are some examples:

• Calculating the volume of a gas: If you know the pressure, temperature, and the number of moles of a gas, you can use the ideal gas law to calculate its volume. For example, if a gas has a pressure of 1 atm, a temperature of 273 K, and 1 mole of gas, its volume can be calculated as:
  

  V = (nRT)/P = (1 mol × 0.0821 L·atm/mol·K × 273 K) / 1 atm = 22.4 L

• Calculating the pressure of a gas: Similarly, if you know the volume, temperature, and the number of moles of a gas, you can calculate its pressure using the ideal gas law. For example, if a gas occupies a volume of 5 L at a temperature of 300 K and contains 2 moles of gas, its pressure can be calculated as:
  

  P = (nRT)/V = (2 mol × 0.0821 L·atm/mol·K × 300 K) / 5 L = 9.85 atm

• Calculating the temperature of a gas: The ideal gas law can also be used to calculate the temperature of a gas if you know its pressure, volume, and the number of moles. For example, if a gas has a pressure of 2 atm, a volume of 10 L, and 3 moles of gas, its temperature can be calculated as:
  

  T = (PV)/(nR) = (2 atm × 10 L) / (3 mol × 0.0821 L·atm/mol·K) = 81.4 K

These examples illustrate how “R” acts as a bridge between the pressure, volume, temperature, and the amount of an ideal gas, enabling us to solve various problems related to ideal gases.

Applications of the Ideal Gas Law

The Ideal Gas Law, a fundamental principle in chemistry and physics, has a wide range of applications in various fields. It is used to predict and explain the behavior of gases in numerous real-world scenarios.

Applications in Chemistry

The Ideal Gas Law plays a crucial role in understanding and predicting the behavior of gases in chemical reactions. It is used to calculate the volume, pressure, temperature, or the number of moles of a gas involved in a reaction. For instance, in a chemical reaction where a gas is produced, the Ideal Gas Law can be used to determine the volume of gas generated under specific conditions.

Applications in Physics

In physics, the Ideal Gas Law is essential for studying the properties of gases and their interactions with other matter. It is used to understand phenomena such as gas expansion, diffusion, and effusion. For example, the Ideal Gas Law can be used to calculate the rate of effusion of a gas through a small hole, a concept crucial in vacuum technology.

Applications in Engineering

Engineers utilize the Ideal Gas Law in various applications, including designing and optimizing systems involving gases. It is used in the design of engines, compressors, and other gas-handling equipment. For instance, in the design of internal combustion engines, the Ideal Gas Law is used to determine the volume of air required for combustion at different engine speeds and loads.

Applications in Meteorology

The Ideal Gas Law is a fundamental tool in meteorology for understanding and predicting weather patterns. It is used to calculate the density, pressure, and temperature of air masses, which are crucial factors in weather forecasting. For example, meteorologists use the Ideal Gas Law to predict the formation of clouds and precipitation.

Applications in Environmental Science

The Ideal Gas Law is used in environmental science to study the behavior of gases in the atmosphere, such as greenhouse gases. It helps to understand how these gases contribute to climate change and develop strategies for mitigating their impact. For example, the Ideal Gas Law can be used to calculate the concentration of carbon dioxide in the atmosphere, a key factor in global warming.

Limitations of the Ideal Gas Law

The Ideal Gas Law is a powerful tool for understanding and predicting the behavior of gases. However, it’s important to recognize that it’s a simplification and doesn’t perfectly represent the behavior of all gases in all conditions. Real gases deviate from ideal behavior, particularly at high pressures and low temperatures.

Deviations from Ideal Behavior

Real gases deviate from ideal behavior because of the following factors:

* Intermolecular Forces: Ideal gases are assumed to have no intermolecular forces, but in reality, real gas molecules do interact with each other. These interactions can be attractive (like van der Waals forces) or repulsive, and they influence the gas’s pressure and volume.
* Finite Molecular Size: Ideal gases are assumed to have zero volume, but in reality, real gas molecules occupy a finite volume. This means that the free space available for the molecules to move around in is less than the total volume of the container.
* Non-Ideal Conditions: The Ideal Gas Law is most accurate at high temperatures and low pressures. At high pressures, the molecules are closer together, and intermolecular forces become more significant. At low temperatures, the molecules have less kinetic energy, and intermolecular forces become more dominant.

Conditions for Ideal Gas Law Accuracy

The Ideal Gas Law is most accurate when the following conditions are met:

* High Temperature: At high temperatures, the kinetic energy of the molecules is much greater than the potential energy due to intermolecular forces. This means that the molecules are moving quickly and are less likely to interact with each other.
* Low Pressure: At low pressures, the molecules are far apart, and intermolecular forces are negligible. This means that the molecules are behaving more like ideal gas molecules.

The Ideal Gas Law is a useful approximation for many real-world applications, but it’s important to be aware of its limitations and to use it appropriately.

Last Point

The ideal gas law, with its constant ‘R’, provides a valuable framework for understanding the behavior of gases. While it has limitations and deviations from real gas behavior, it serves as a powerful tool in numerous fields, including chemistry, physics, and engineering. By understanding the role of ‘R’, we gain a deeper appreciation for the interconnectedness of gas properties and the predictive power of this fundamental law.

Clarifying Questions: What Is The R In The Ideal Gas Law

What is the numerical value of the ideal gas constant ‘R’?

The numerical value of ‘R’ depends on the units used for pressure, volume, and temperature. The most common value is 0.0821 L·atm/mol·K.

Why is ‘R’ called the ideal gas constant?

It’s called the ideal gas constant because it’s a proportionality constant that links the variables in the ideal gas law, which is a simplified model for gas behavior.

How does the value of ‘R’ change with different units?

The value of ‘R’ changes depending on the units used for pressure, volume, and temperature. For example, using SI units (Pa, m³, K) gives ‘R’ a value of 8.314 J/mol·K.

What are some real-world applications of the ideal gas law?

The ideal gas law is used in various applications, such as calculating the volume of a gas at a given temperature and pressure, determining the pressure of a gas in a container, and predicting the behavior of gases in chemical reactions.